
Weight reduction is a key design focus in many applications. This is particularly true in the automotive industry, where lightweight materials help foster the development of fuel efficient cars. Maintaining the structural integrity of these materials is, of course, an important concern. As we will show you today, simulation is a valuable tool for addressing this challenge.
A Light Solution with a Heavy Impact
With gas prices and environmental concerns on the rise, a heightened demand for energy efficient vehicles has emerged in recent years. In response to this growing demand, the automotive industry has turned to alternate design approaches for automobiles, one of which is using lightweight materials.
Compared to their heavier counterparts, lightweight automobiles not only feature a simplified design structure, but they are also more energy efficient. In fact, according to the Office of Energy Efficiency & Renewable Energy, reducing vehicle weight by 10% can lead to a fuel economy improvement of up to 8%.
While the lightest weight possible is ideal, designers and engineers must ensure that reducing the weight of a vehicle’s component does not impact its structural integrity. These lighter components must still be able to perform their designed function efficiently and resist failure. Using the example of a mounting bracket, we will demonstrate how simulation can help develop an optimal design that meets such requirements.
Enhancing the Structural Design of a Lightweight Mounting Bracket
The Multistudy Optimization of a Bracket tutorial, available in our Application Gallery, features a bracket made of steel that supports a mounted component. When compared to the bracket, the mounted component can be observed as rigid.
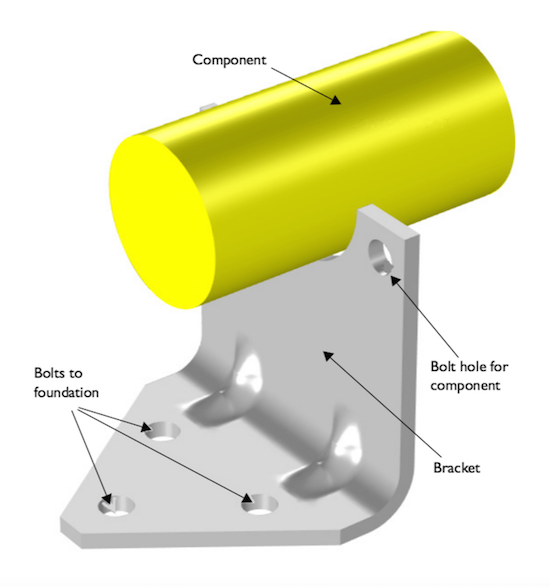
The bracket (shown in gray) supports a heavy component (shown in yellow).
Because the bracket mounts the heavy component on a vibrating foundation, it is important that the natural frequency is maintained well above the excitation frequency. This will help avoid resonances. The shock loads that are applied to the bracket can be treated as a static acceleration load. The result? An optimization problem where our objective is to reduce the weight of the bracket, which is subjected to constraints on the natural frequency, maximum stress due to shock loads, and material dimensions. This means that the optimization problem should be solved over two different types of analyses: eigenfrequency and stationary.
To reduce the weight of the bracket, we drill holes into its vertical surface. At the same time, to offset the loss in stiffness, we alter the dimensions of the indentations. Six different geometrical parameters, summarized in the figure below, are included in the optimization.
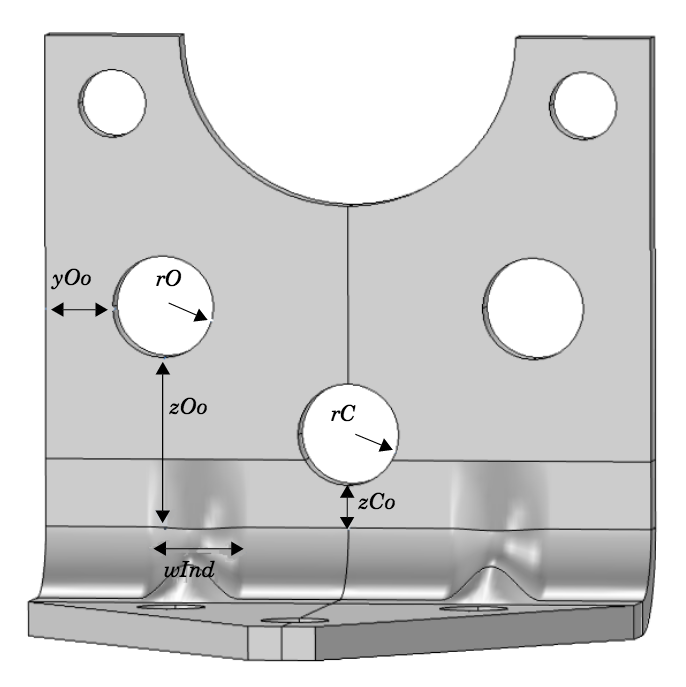
Geometrical parameters used in the bracket’s structural optimization.
A series of geometrical constraints are applied to our simulation to ensure that the bracket geometry remains feasible. They are the following:
- The lowest natural frequency must be a minimum of 60 Hz
- The equivalent stress cannot exceed 80 MPa when exposure to a peak acceleration of 4g occurs in all three global directions at once
- There needs to be a minimum of 3 mm of material between two holes or a hole and an edge
The optimal geometrical parameters for our lightweight bracket are illustrated below. As you can see, three small holes have been introduced into the geometry. In its optimized state, the bracket weighs 178 g, which is 27 g less than its original weight.
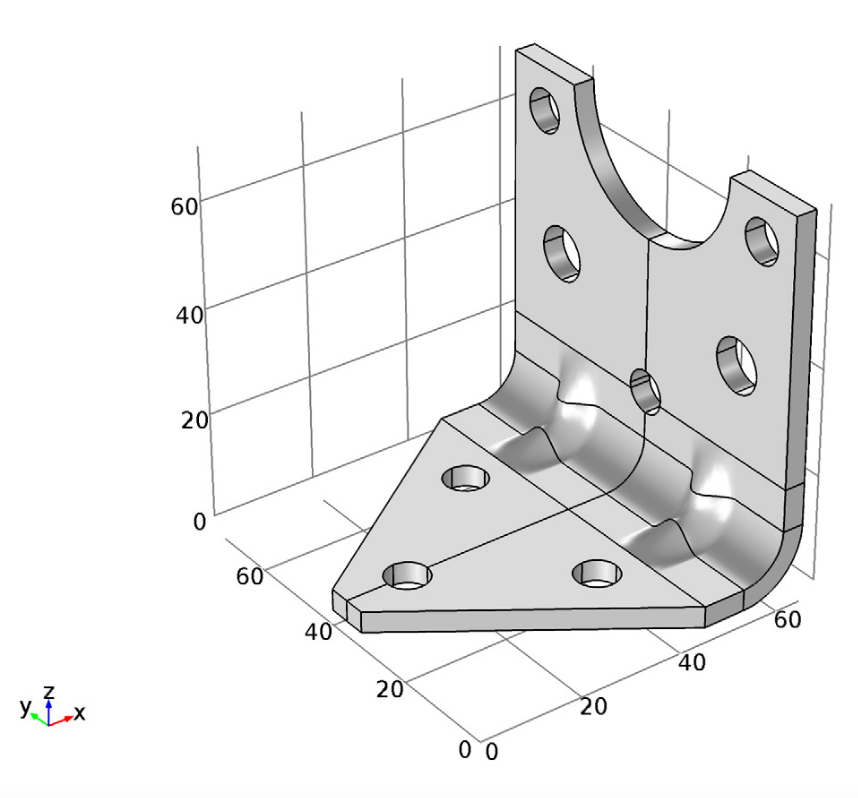
Initial optimization geometry.
Let’s now shift focus to addressing our constraints, particularly the shock load applied to the bracket. Looking at the results in the plot below, we can see that the stress is less than 80 MPa on the entire geometry. As such, this bracket design successfully meets its stress constraint, balancing weight reduction with functionality.
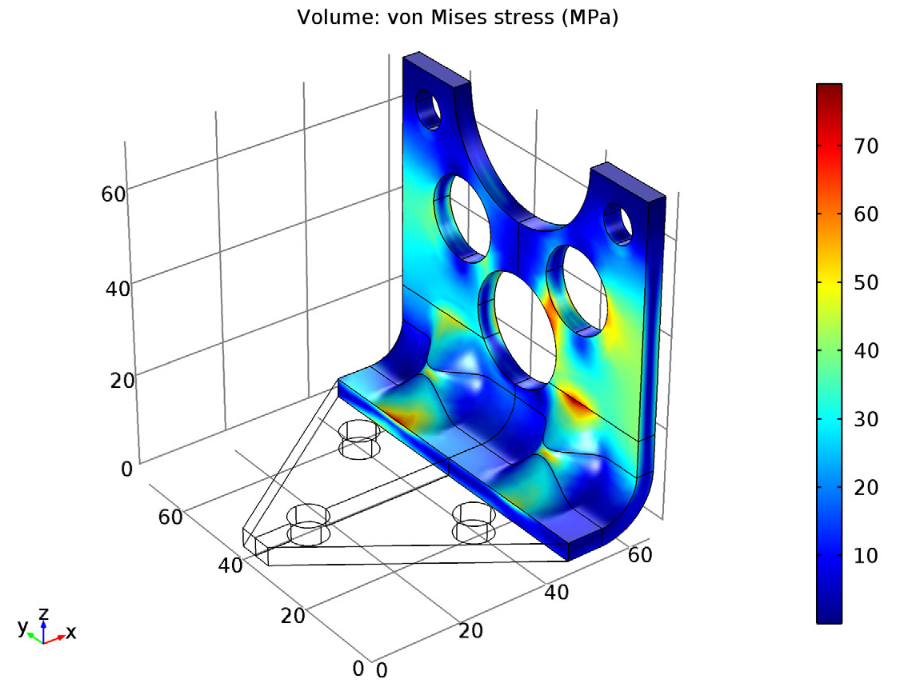
The stress from a shock load (peak acceleration) on the optimized bracket.
While the optimal solution here includes three rather large holes and the widest indentation possible, note that other possible hole arrangements offer the same degree of weight reduction within a small tolerance. Thus, the design variables may differ at convergence.
Further Reading
- Download the tutorial model: Multistudy Optimization of a Bracket
- Check out the other blog posts within our Optimization category




Comments (0)