
As two of the greatest mathematicians to have ever lived, Leonhard Euler and Joseph-Louis Lagrange made numerous contributions to continuum mechanics. Combining their individual descriptions of the subject inspired the arbitrary Lagrangian-Eulerian (ALE) method, a technique that can be used for a multitude of simulation applications. Find out how the work of Euler and Lagrange helped create the ALE method and how it aids your simulations in the COMSOL Multiphysics® software.
Leonhard Euler and Joseph-Louis Lagrange
Born in 1707 in Basel, Switzerland, Leonhard Euler (pronounced “oiler”) was a prolific mathematician who published more than 800 articles during his lifetime. He studied under the famous Johann Bernoulli and received his master’s degree in philosophy from the University of Basel. Before moving to St. Petersburg, Russia, to work at the university, Euler submitted his first paper to the Paris Academy of Sciences, coming in second place at only 19 years old.

A portrait of Leonhard Euler. Image in the public domain, via Wikimedia Commons.
Euler quickly rose through the academic ranks and in 1733 succeeded Bernoulli as the chair of mathematics in St. Petersburg. Euler moved to Berlin in 1741 at the invitation of King Frederick II. In his 25 years there, he wrote around 380 articles and the first volume of his seminal book Introductio in Analysin Infinitorum, which formally defined functions for the first time; introduced the f \left( x \right) notation; popularized the e and \pi notation; and established the critical formula e^{i\theta} = \cos \left( \theta \right) + i \sin \left( \theta \right).
Joseph-Louis Lagrange (pronounced “luh-gronj”) was born Giuseppe Lodovico Lagrangia in Turin. Today, this city is the capital of the region of Piedmont in Italy, but when Lagrange was born in 1736, it was ruled by the Duke of Savoy as part of the Kingdom of Sardinia. Lagrange developed an interest in mathematics and, after working independently on novel topics, began corresponding with Euler, whom he succeeded when Euler left Berlin.

A portrait of Joseph-Louis Lagrange. Image in the public domain, via Wikimedia Commons.
In Berlin, Lagrange developed most of the mathematics for which he is famous today. He played an important role in the development of variational calculus and came up with the Lagrangian approach to mechanics. Although Lagrangian mechanics makes the same predictions as Newton’s laws of motion, the Lagrangian functional introduced by Lagrange allows the classical mechanics of many problems to be described in a mathematically more straightforward and insightful manner than in Newtonian mechanics. Lagrange also developed the method of Lagrange multipliers, which allows constraints on systems of equations to be introduced easily in a variational approach.
Comparing the Eulerian and Lagrangian Methods
The mathematical formulations of Euler and Lagrange are fundamental to the finite element method, which is used to solve equations in COMSOL Multiphysics.
In the Eulerian method, the dynamics of a system are considered from the viewpoint of an observer measuring the system’s evolution with respect to a fixed system of coordinates. This coordinate system is called the spatial frame in COMSOL Multiphysics. It could be understood to correspond to the laboratory frame in physical analysis, since the system of coordinates is oriented according to a fixed set of axes without any reference to the orientation of the components of the physical system itself.
The figure below illustrates a thin plate of material whose structural mechanics are modeled in a 2D plane. The plate is fixed to a rigid wall at the left-hand side and is deformed under its own weight, as gravity acts downward. With the results plotted in the spatial frame, we see the deformation of the object, as we would expect to observe in the laboratory.
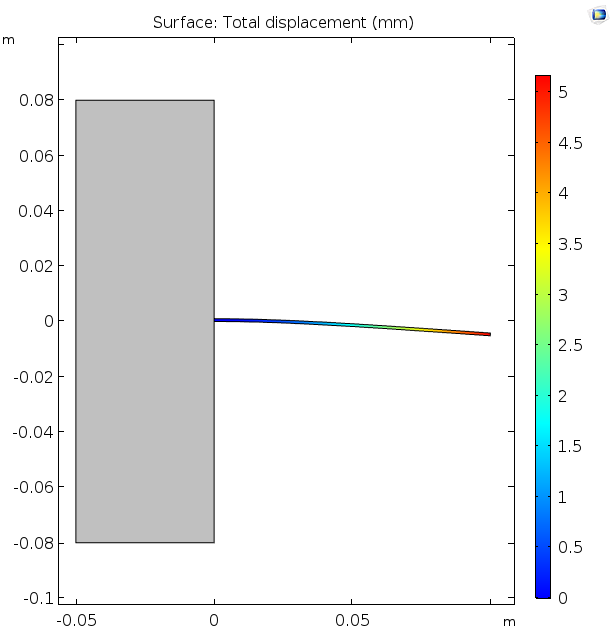
A thin plate fixed to the gray block at the left deforms under its own weight, as viewed in the spatial (lab) frame. The deflection at the tip is about 5 mm for the given mechanical properties.
Formulating physical equations seems very natural in the Eulerian method. Indeed, this is the common formulation for problems such as electromagnetics and fluid physics, in which the field variables are expressed as functions of the fixed coordinates in the spatial frame.
For mechanical problems, though, the Lagrangian method offers a helpful alternative. In the Lagrangian method, the mechanical equations are written with reference to small individual volumes of the material, which will move within an object as it displaces or deforms dynamically. To put it another way, the object itself always appears undeformed from the point of view of the Lagrangian coordinate system, since the latter stays attached to the deforming object and moves with it, but external forces in the surroundings appear to change their orientation from the deforming object’s perspective. The corresponding coordinate system, which moves along with the deforming object, is called the material frame in COMSOL Multiphysics.
A point within the object, as measured in the spatial frame, is displaced from the position of the same point as expressed in the material frame by the mechanical displacement of that point. In the image below, we focus our view on the tip of the deforming plate in the example above and animate its deformation as the density of the object increases so that the weight increases too. As you can see, the material frame coordinate system (red grid and arrows) deforms together with the object, as the object’s dimensions in the spatial frame change. This means that anisotropic material properties — such as mechanical properties of composite materials — can be expressed conveniently in the material frame.
Zoomed-in view of the tip of a thin plate deforming under its own weight, as its density is increased. The red grid denotes the material frame coordinates, tied to the object, as viewed in the spatial (lab) frame. The red and green arrows show the x– and y-coordinate orientations of the material frame, as viewed in the spatial frame.
In the limit of very small strains for this type of mechanical problem, the spatial and material frames are nearly coincident, because the mechanical displacement is small compared to the object’s size. In this case, it is common to use the “engineering strain” to define the elastic stress-strain relation for the object, and the resulting stress-strain equations are linear. As the mechanical displacement increases, though, the linear approximation used to evaluate the engineering strain is increasingly inaccurate — the exact Green-Lagrange strain is required. In COMSOL Multiphysics, the term “geometric nonlinearity” means that the Green-Lagrange strain is used.
For further details on the mathematics, see my colleague Henrik Sönnerlind’s blog post on geometric nonlinearity.
Geometric nonlinearity is handled in COMSOL Multiphysics by allowing the spatial frame to be separated from the material frame, according to a frame transformation due to the computed mechanical displacement. It remains convenient to access the material frame to express properties such as anisotropic mechanical material properties, since these properties will usually remain aligned with the material frame coordinates, even as the object deforms.
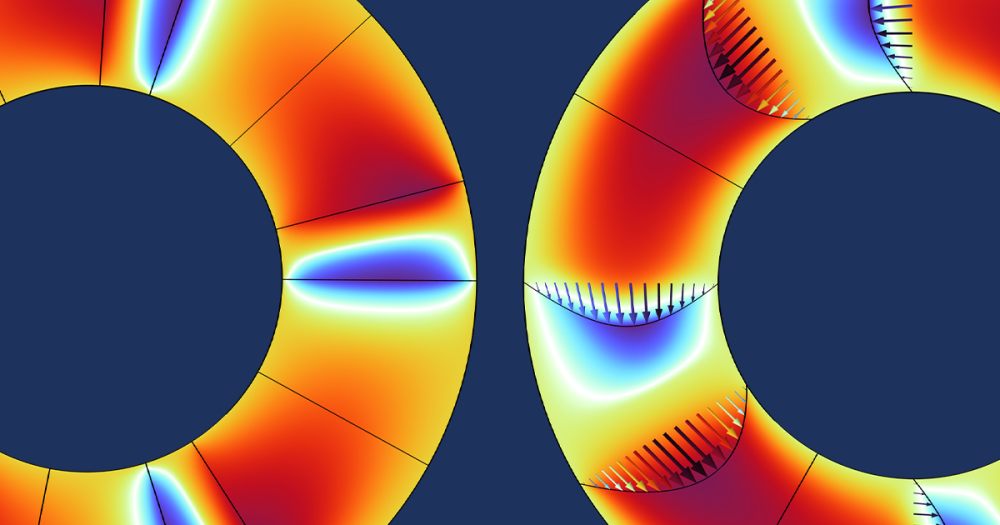
By contrast, external forces such as gravity have a fixed orientation in the spatial frame. From the perspective of the material frame, external forces like gravity change direction as the object deforms. The image below shows the tip of the thin plate as above, but here, the displacement magnitude is plotted with colors. Arrows are used to illustrate the force due to gravity, as expressed in the material frame coordinates. Since the material frame coordinates remain fixed with respect to the object, the dimensions of the object appear not to change. However, the displacement magnitude increases with the object’s weight and the gravity force increasingly changes direction with respect to the deformed material in conditions of greater deformation.
Zoomed-in view of the tip of a thin plate deforming under its own weight as its density increases. The plot is in the material frame as used for the Lagrangian formulation, so the deformation is not apparent, although displacement increases. The red arrows indicate the apparent direction of gravity (which is constant in the spatial frame) as perceived from the material frame of reference within the deforming object.
Neither the Lagrangian nor Eulerian formulation is more “physical” or “correct” than the other. They are simply different mathematical approaches to describing the same phenomena and equations. Through coordinate transformation, we can always transform the physical equations for any phenomenon from the material frame to the spatial frame or vice versa. From the perspective of interpretation and implementation, though, each approach has certain advantages and common applications. Some of these are summarized in the table below:
| Strengths | Common Applications | |
|---|---|---|
| Eulerian Method |
|
|
| Lagrangian Method |
|
|
What Is the ALE Method?
What about multiphysics problems, such as fluid-structure interaction (FSI) or geometrically nonlinear electromechanics? In these cases, one physical equation might be formulated most naturally with the Eulerian method, while another might be better expressed with the Lagrangian method. This is where the ALE method comes in. This method solves the equations on a third coordinate system, which is not required to match either the spatial frame or the material frame coordinate systems.
The third coordinate system is called the mesh frame in COMSOL Multiphysics. There is one mathematical mapping between the spatial frame and the underlying mesh frame, and one between the material frame and the underlying mesh frame, so at all points in time, the equations formulated in the spatial and material frames can be transformed into the mesh frame to be solved.
In domains representing solids in a model, mechanical displacement is predicted using structural mechanics equations in the Lagrangian formulation. Here, the relation of the spatial and material frames is given by the mechanical displacement, as above. The ALE method adds more equations to allow the apparent positions and shapes of mesh elements in neighboring domains to displace in the spatial frame. That is in order to account for how mechanical deformation can change the shape of the boundaries of any domain where the physics are described in the Eulerian formulation. These additional equations are called a Moving Mesh or Deformed Geometry in COMSOL Multiphysics.
At boundaries between Lagrangian and Eulerian domains, a boundary condition for these additional equations requires that the displacement of the spatial frame (as defined through the moving mesh) for the Eulerian domain must match the mechanical displacement of the spatial frame away from the material frame in the Lagrangian domain. Even where no mechanical equations are solved, such that no Lagrangian method is used, the ALE method can still be used to express moving boundaries due to deposition or loss of material.
Applying the ALE Method in Multiphysics Modeling
If you find the ALE method quite mathematical, that’s OK! It’s a difficult concept to follow in the abstract. To better understand the way the ALE method works, let’s take a look at an example within COMSOL Multiphysics.
Fluid-Structure Interaction in a Micropump Mechanism
The ALE method plays an important role in modeling FSI. In COMSOL Multiphysics, this method enables the automated bidirectional coupling of fluid flow and structural deformation, a capability demonstrated in our Micropump Mechanism tutorial model.
At the heart of this micropump mechanism are two cantilevers, which perform the same function as valves in conventional pumping devices. These cantilevers are flexible enough that the fluid flow causes them to deform. As fluid is alternately pumped into or out of the channel at the top, the force of the fluid flow causes the two cantilevers to deform so that fluid flows out to the right or in from the left.
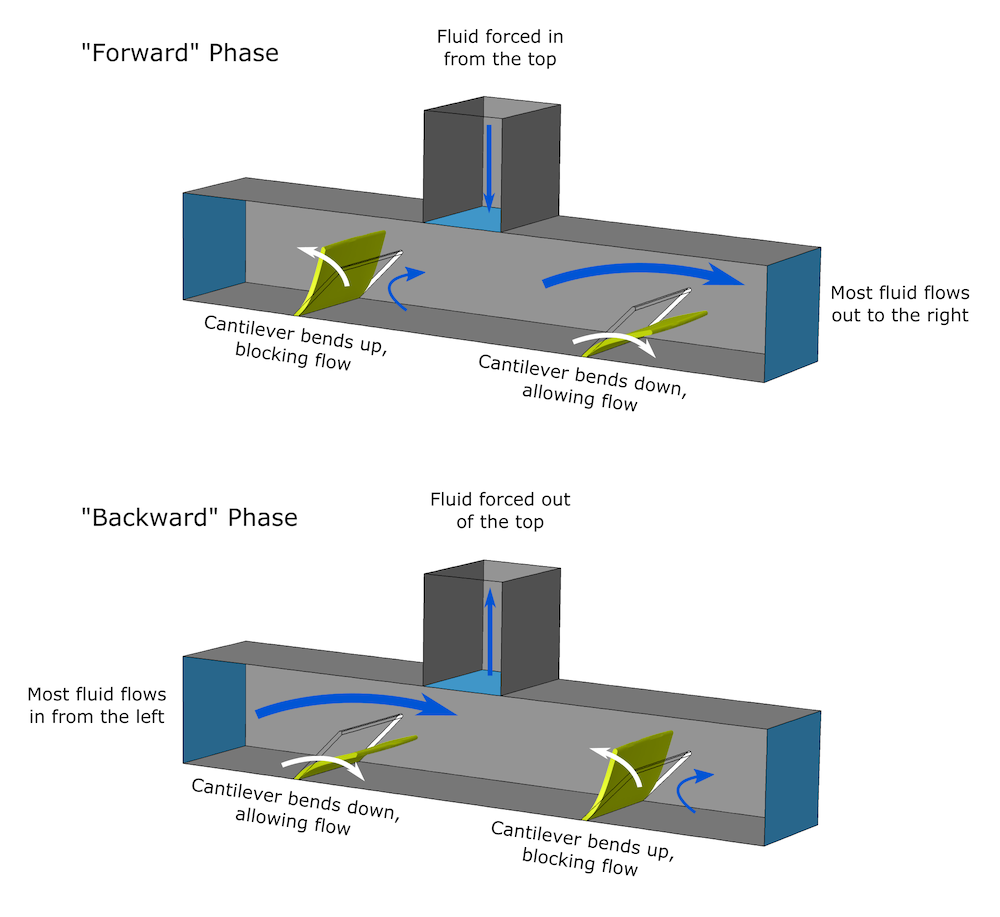
The micropump mechanism. Pumping fluid into or out of the top tube produces opposite reactions in the two cantilevers, pushing fluid in or out of the chamber. Even though there is no time-averaged net flow into the upper tube, there is a time-averaged net movement of fluid from left to right.
The cantilevers deform enough that there is an appreciable change in the position of the boundary where the fluid and solid meet: a geometrically nonlinear case. The self-consistent handling of the fluid’s pressure on the solid and the solid’s force on the fluid, together with the deformation of the mesh, are handled automatically by the Fluid-Structure Interaction interface. The interface employs the ALE method to account for the change in shape in the solid and fluid regions.
For solids, the mechanical equations with geometric nonlinearity define the displacement of the spatial frame with respect to the material frame. In the fluid equations, it’s necessary to deform the mesh on which the equations are solved in order to express the displacement of the solid boundaries in the spatial frame where the fluid equations are formulated. The deformation at the boundaries is controlled by the mechanical displacement from the solution to the structural problem. Within the fluid, though, the exact position or orientation of mesh nodes isn’t important, as the equations are formulated in the fixed spatial frame. Instead, the deformation of the mesh is smoothed in order to ensure that the numerical problem remains stable with high-quality mesh elements.
To explain the ALE method for the FSI problem, we could paraphrase a common explanation for general relativity: forces due to fluid flow (Eulerian) tell the structure how to deform in the material frame (Lagrangian), while the structural deformation (Lagrangian) tells the mesh how to move in the spatial frame (Eulerian).
Top: The micropump’s operation, including pressure, flow, and cantilever deformation, as plotted in the spatial frame. Bottom: Mesh deformations calculated by the ALE method.
As of COMSOL Multiphysics version 5.3a, the Moving Mesh feature to define mesh deformation in this type of problem is located under Component > Definitions. This allows consistency in the definition of material and spatial frames between all physics included in a model, even if several physics interfaces are included. The screen capture below shows where these settings are located in the COMSOL Multiphysics Model Builder tree.
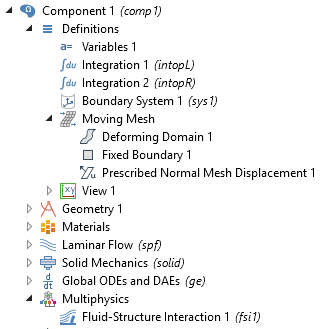
Screen capture showing Moving Mesh features under Component > Definitions, and physical coupling between two physics interfaces through Multiphysics > Fluid-Structure Interaction.
Electrodeposition in a Copper Trench
Turning to an electrochemical problem, the Copper Deposition in a Trench tutorial model shows that the ALE method can be vital for simulating electrodeposition problems. In this model, copper is deposited onto a circuit board that has a small “trench”. The deposited copper layer becomes thick compared to the overall size of the trench, so the size and orientation of the copper surface change appreciably as deposition proceeds. Since the rate of copper deposition at different points on this surface is nonuniform, the shape and movement of the boundary cannot be neglected.
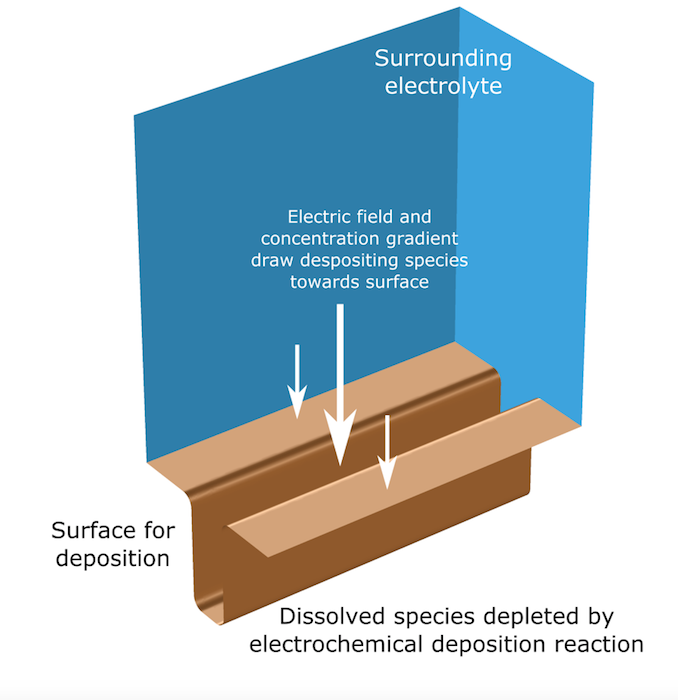
A schematic of the physical problem being solved in the electrodeposition model.
To calculate the rate of deposition at a given point on the copper electrode-electrolyte interface, we need the concentration of the species and the electrolyte potential of the solution adjacent to that point. As the deposition progresses and the boundary moves, the shape of the electrolyte volume has to change continuously. Similarly, the concentration and potential distributions on the altered shape must be recalculated.
The coupling of the deposition rate to the boundary motion rate and the calculation of the changing shape are accomplished with the ALE method and fully automated multiphysics couplings with the Tertiary Current Distribution and Deformed Geometry interfaces. Here, the Deformed Geometry displaces the copper surface in the spatial frame at a rate proportional to the local current density for electrodeposition, as computed from the electrochemical interface.
With this model, we can accurately account for the deposition process in order to optimize its parameters. We can also experiment with different applied potentials and deposition surface geometries to improve the uniformity of the deposition, which produces a more efficient process and a higher-quality end product.
Animations showing the evolution of the deposition process in time. It is clear that the deposition happens unevenly, resulting in a pinching of the trench opening at its top.
Thermal Ablation
Thermal ablation, discussed in this previous blog post, involves a very high temperature applied to an object, causing the surface to melt and vaporize. Examples of thermal ablation include the removal of material by lasers — such as in the etching process, laser drilling, or laser eye surgery — and a spacecraft’s heat shield as it reenters the atmosphere.
Animation showing the effect of thermal ablation on a material.
Since we expect that an object’s shape will change when some of its material is removed, deforming meshes are clearly a key part of thermal ablation simulation. What we need to know is how the shape of the object will change. This depends on how we balance the applied heat with heat lost to ablation and heat dissipation throughout the structure by mechanisms such as conduction.
To obtain this information, we can predict the temperature profile as a function of space and time by solving the heat transfer equations using the Heat Transfer interface. Because the mass and shape of the object are changing, the Heat Transfer interface is coupled to a Deformed Geometry interface, using the ALE method to displace the boundary according to the rate of ablation. The Heat Transfer equations predict the temperature distribution in the object as its shape evolves.
By performing these steps, we can attain accurate calculations for the thermal ablation process. Moreover, we can determine the final shape of the object after ablation is complete. This might enable us to check whether a laser weld will fall within acceptable tolerances or whether a spacecraft will survive an emergency landing.
Using Deformed Meshes in Your Simulations
The contributions of Leonhard Euler and Joseph-Louis Lagrange in the field of mathematics have paved the way for simulating a variety of systems involving multiphysics applications. The combination of their individual methods has led to the development of the ALE method, which can be used to predict physical behavior when objects deform or displace. By properly accounting for these movements, you can set up highly accurate models. Remember to thank Euler and Lagrange as you investigate these and other models that exploit the ALE method!
The ALE method is one of many built-in physics capabilities in the COMSOL Multiphysics® software. See more of them:
Resources on the Arbitrary Lagrangian-Eulerian Method
- Access the tutorial models featured in this blog post:
- Learn how to use the ALE method to model linear and rotational displacements and arbitrary translational motion:





Comments (2)
Tianyu Yang
June 3, 2021Dear Edmund,
Thank you for sharing this. I am working on fully-coupled thermal expansion and heat transfer problem. The obstacle is that the solid deformation by thermal expansion is not considered to affect heat transfer by default settings. I am wondering if I should apply the ALE interface to solve the heat transfer in the deformed solid domain.
Thank you!
Tianyu
Brianne Christopher
June 4, 2021Hi Tianyu,
Please contact support@comsol.com for assistance with your modeling problem.
Best,
Brianne