
When ambient air flows through porous media, it carries moisture. In this process, temperature and moisture are coupled: The vapor saturates depending on the temperature conditions, while latent heat effects due to evaporation and condensation modify the temperature. We discussed heat and moisture transport in air in a previous blog post. Let’s address the specific transport processes we need to consider in pores and how to model heat and moisture transport in porous media with the COMSOL Multiphysics® software.
Modeling Heat and Moisture Transport in Building Materials
Building physics engineers aim to improve the energy performance and sustainability of building envelopes. Although their practices are based on past experience, new materials and building techniques are constantly being developed that offer a wide set of options in building design and thermal management. Let’s see how to model heat and moisture transport in building materials to help reduce energy costs and preserve buildings.
Building envelopes can be analyzed by modeling heat and moisture transport.
Controlling moisture is necessary to optimize the thermal performance of building envelopes and reduce energy costs. The thermal properties of insulation or isolation materials usually depend on both temperature and moisture content. Therefore, a coupled heat and moisture model helps us fully analyze the thermal performance of a building component. One example is the dependence of a lime silica brick’s thermal conductivity on relative humidity.
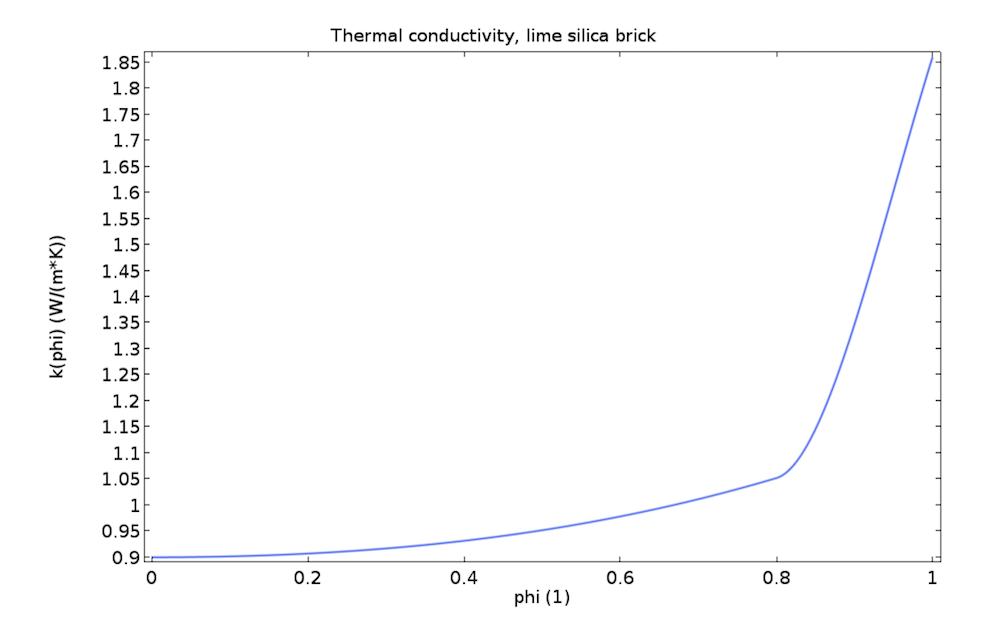
The moisture dependence of thermal conductivity for lime silica brick.
The figure above shows that lime silica brick becomes two times less thermally isolating for high relative humidity values.
In addition, we must consider moisture control in the building design process to choose building components that can reduce the risk of condensation. The coupled modeling of heat and moisture transport enables us to analyze different moisture variations and phenomena in building components, such as:
- Drying of moisture resulting from the initial construction
- Condensation due to the migration of moisture from outside to inside during warmer periods
- Moisture accumulation by interstitial condensation due to vapor diffusion during colder periods
Let’s consider a wood-frame wall between a warm indoor environment and a cold outdoor environment. Vapor diffuses through the wall from the high-moisture environment inside to the low-moisture environment outside. This creates high relative humidity values associated with low temperature values close to the exterior panel, with the risk of condensation as a direct consequence.
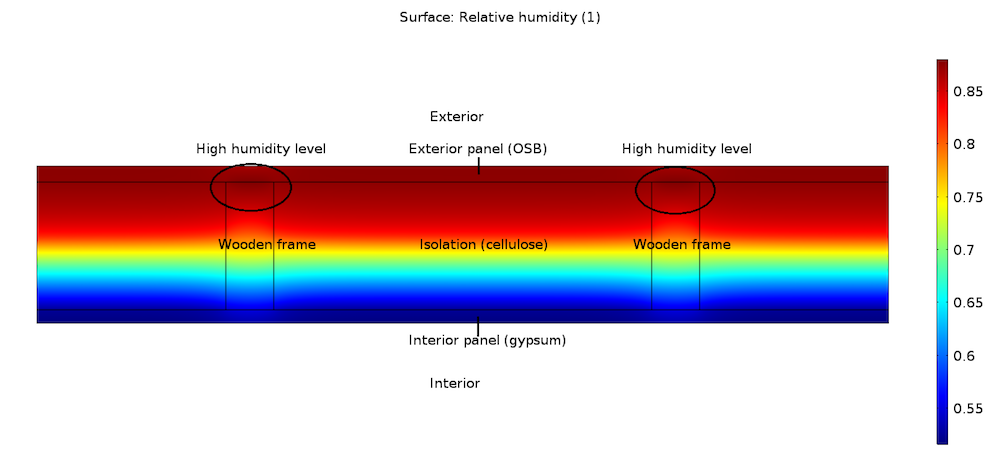
The relative humidity distribution in a wood-frame wall.
Condensation leads to mold growth, which directly affects human health and building sustainability. The rate of mold growth is key data for the preservation of historical buildings, for example. To prevent the risk of interstitial condensation, it is common practice to add a vapor barrier between the interior gypsum panel and the cellulose isolation board. This reduces the moisture values where they are at a maximum. The figure below shows the relative humidity distribution across the wood-frame wall through a wood stud (red lines) and a cellulose board (blue lines), with and without the vapor barrier (dashed lines and solid lines, respectively).
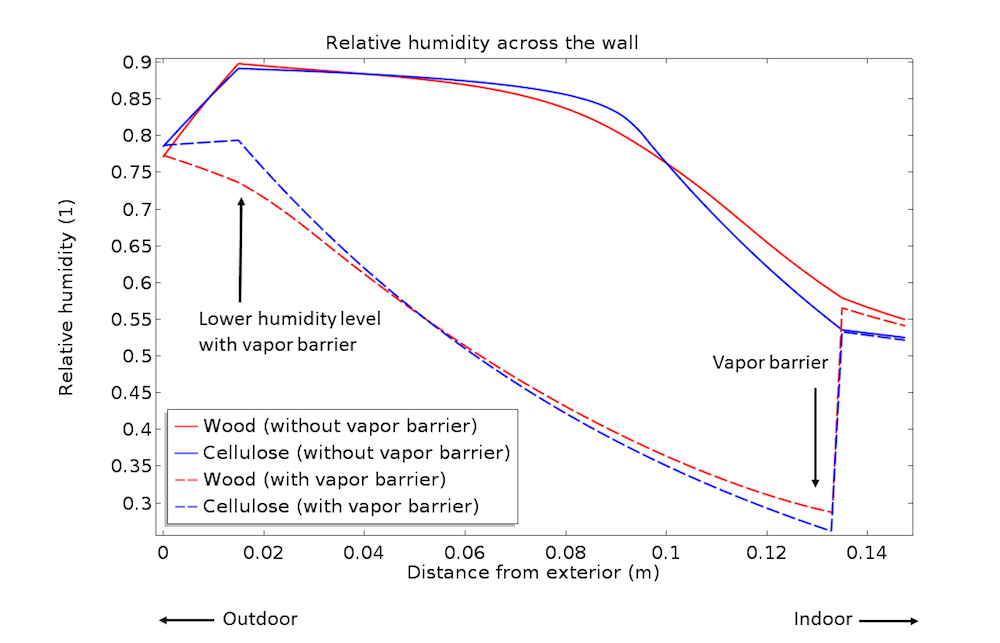
Effect of a vapor barrier on relative humidity distribution across the wood-frame wall in a wood stud and cellulose board.
For this model, we consider the building materials to be specific unsaturated porous media in which the moisture exists in both liquid and vapor phases and only some transport processes are relevant. The norm EN 15026 standard addresses the transport moisture phenomena that is taken into account in building materials, following the theory expressed in Ref. 1.
The transport equation established as a standard by the norm accounts for liquid transport by capillary forces, vapor diffusion due to a vapor pressure gradient, and moisture storage.
We model the latent heat effect due to vapor condensation by adding the following flux in the heat transfer equation:
In addition, the moisture dependence of the thermal properties is assessed.
Find details about the moisture transport equation in building materials in the Heat Transfer Module User’s Guide.
When using the Heat Transfer Module, the Heat and Moisture Transport interface adds a:
- Heat and Moisture coupling node
- Heat Transfer in Building Materials interface
- Moisture Transport in Building Materials interface
- Building Material feature for heat transfer
- Building Material feature for moisture transport
- Thin Moisture Barrier feature for modeling the vapor barrier
Finally, the latent heat source due to evaporation is added to the heat transfer equation by the Building Material feature of the Heat Transfer interface.
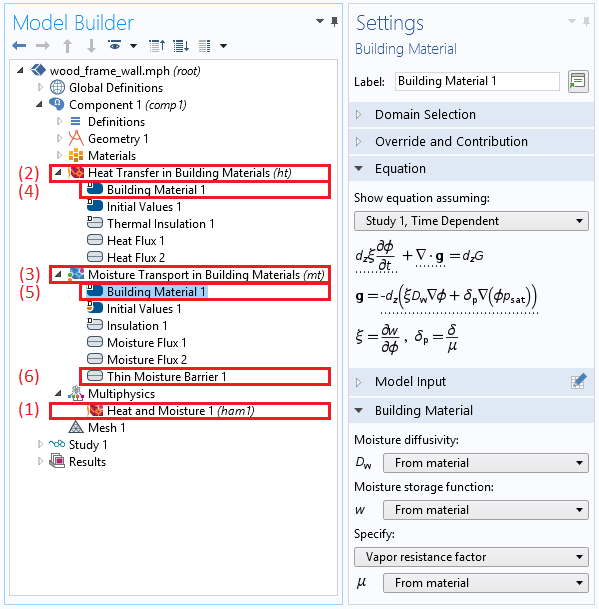
The model tree and subsequent subnodes when choosing the Heat Transfer in Building Materials interface, along with the Settings window of the Building Material feature.
Coupled Modeling of Heat and Moisture Transport in Unsaturated Porous Media
Modeling heat and moisture transport in an unsaturated porous medium is important for analyzing polymer materials for the pharmaceutical industry, protective layers on electrical cables, and food-drying processes, to name a few examples.
For these applications, phenomenological models, such as the one presented above for building materials, may not be available. However, by considering the conservation of heat and moisture in each phase (solid, liquid, and gas), and volume averaging over the different phases, we can derive a mechanistic model.
To compute the moisture distribution, we solve a two-phase flow problem in the porous medium. Two equations of transport are solved: one for the vapor and one for the liquid water. The coupling between the vapor and liquid water operates through the definition of saturation variables, Svapor + Sliquid = 1. The changing water saturation is taken into consideration for the definition of the effective vapor diffusivity and liquid permeability.
For quick processes, with a time scale comparable to the time it takes to reach equilibrium between the liquid and gas phases inside the pores of the medium, a nonequilibrium formulation can be defined through the following evaporation flux:
In this definition, the equilibrium vapor concentration, defined as the product of the saturation concentration csat and the water activity aw, is used to account for the porous medium structure. Indeed, due to capillary forces, equilibrium is reached for concentrations that are lower than in a free medium.
By letting the evaporation rate K go to infinity, an equilibrium formulation is obtained with the vapor concentration equal to the equilibrium concentration.
Let’s consider a food-drying process. A piece of potato, initially saturated with liquid water, is placed in an airflow to be dried. Inside the potato, the vapor is transported by binary diffusion in air. We use a Brinkman formulation to model the flow induced by the moist air pressure gradient in the pores. As the liquid phase velocity is small compared to the moist air velocity, Darcy’s law is used for the liquid water flow due to the pressure gradient. The capillary flow, due to the difference between the relative attraction of the water molecules for each other and the potato, is also considered in the liquid water transport.
The vapor and liquid water distributions over time for this model are shown in the following two animations. Note that water can leave the potato as vapor only.
The liquid water concentration over time.
The vapor is transported away by the airflow, as shown in this animation:
The water vapor concentration over time.
The evaporation causes a reduction of the temperature in the potato. The temperature distribution over time is shown below.
Temperature distribution over time.
You can implement the equations in the Heat Transfer in Porous Media interface within the Heat Transfer Module and the Transport of Diluted Species interface within the Chemical Reaction Engineering Module. This process requires some steps in order to couple the multiphase flow in a porous medium together with the evaporation process.
Read the article “Engineering Perfect Puffed Snacks” on pages 7–9 of COMSOL News 2017 to see how Cornell University researchers used COMSOL Multiphysics to model rice puffing. In this numerically challenging process, the rapid evaporation of liquid water results in a large gas pressure buildup and phase transformation in the grain.
Closing Remarks on Modeling Heat and Moisture Transport in Porous Media
In this blog post, we discussed COMSOL® software features for modeling heat and moisture transport in porous media. COMSOL Multiphysics (along with the Chemical Reaction Engineering Module and Heat Transfer Module) provides you with tools to define the corresponding phenomenological and mechanistic models for a large range of applications. Depending on the dominant transport processes, you can use predefined interfaces or define your own model.
Reference
Künzel, H. 1995. Simultaneous Heat and Moisture Transport in Building Components. One and two-dimensional calculation using simple parameters. PhD Thesis. Fraunhofer Institute of Building Physics.
Try It Yourself
- Check out the tutorial models featured in this blog post:






Comments (14)
Rahul Singh
January 11, 2018Thanks for your kind information. Here i want to know one more thing that, is there any possibility to study/analyse the hygro-thermal effects on vibration of functionally graded beams.
Thanks/regards
Rahul Singh
(PG Scholar)
Claire Bost
January 11, 2018Hi, it should be possible to add a structural mechanics computation in which the Young modulus will be set as a function of the relative humidity computed in the heat and moisture transfer problem. However, there is no predefined physics interface for that.
Bowei Yu
January 28, 2018Hi Claire,
Your blog is very helpful and thank you for your work.
I am currently dealing with a THM model in soil, where includes the water-vapor transportation under temperature gradient in an unsaturated soil column.
I’ve tried to use PDE module to build up my own model, however, it is very difficult to get a convergent calculation result. Do you think it can be done using the predetermined modules?
Regards
Bowei Yu
PhD student from Sydney
Claire Bost
January 29, 2018Hi Bowei,
On the side of the predefined interfaces, there is the Transport of Diluted Species in Porous Media interface, that can be applied to a partially saturated porous medium. You can use it twice in your model, once with the liquid phase, once with the gas phase, and then couple the two sets of equations through saturation conditions. I suggest that you have a look at the “Evaporation in Porous Media with Large Evaporation Rate” model that you can find in the Application Library, Heat Transfer>Phase Change branch. But you’re right, the convergence of a model solving for both phases is more challenging than for a model solving for relative humidity.
Best Regards,
Claire
Bowei Yu
February 13, 2018Hi Claire,
Many thanks to your suggestion. Results turns out better than building my own PDEs, at least convergence is much easier to get.
Best regards
Bowei
How-Ming Lee
June 5, 2018Thanks for a very good application. As you mentioned, “K” is an evaporation rate depending on the application. I had found that “K” significantly affects the evaporation amount and heat. In COMSOL’s examples, the “K” is always set as a constant. However, “K” should be varied with the time, since the temperature difference between the water-containing media and the gas is getting small along the time. And the “K” should be varied with the temperature, the gas flow rate, etc. Could you share where to find detail information on how to determine the evaporation rate. Thank you very much.
Claire Bost
June 25, 2018Hi,
For the definition of K in function of the temperature, the Hertz-Knudsen equation may be used. It is based on the kinetic theory to express the mass flux on flat interfaces.
This expression can be set for the K user input.
Also, the Chilton–Colburn analogy is implemented since Version 5.3a in the Moisture Flux boundary condition. For a set of different flow (natural/forced convection) and geometry conditions, you can obtain the convective heat transfer coefficient from correlations based on Nusselt number, and the analogy is applied to compute the moisture transfer coefficient.
Farjallah Alassaad
April 26, 2019Thank you for your application. i am a student doing an intership, and i have a part of intership to estimate numerically the effect of evaporation on porous materiel. I have one small question. you consider the porosity 0.8 in the example of “Evaporation in Porous Media with Large Evaporation Rate” and the initial RH in the solid is 100%, but the porosity on concrete for example should be less, so when i change the porosity to 0.3, the initial RH change to 50%. i think that there is another parameter should be changed when we change the porosity, and i think they are the initial water saturation and the irreductible liquid phase saturation but i don’t find article on how it depend from the porosity. am i right? how these parameter change over the porosity?
Thank you very much
Claire Bost
April 29, 2019Hi,
If you want to keep the same amount of moisture content while reducing the porosity of the material, you can play with both the relative humidity and the saturation. The relative humidity is related to the vapor pressure in the gas phase, whereas the saturation describes the amount of each phase (liquid/gas).
The irreductible liquid phase saturation is introduced in the model for the expression of the relative permeability for liquid phase. It comes from the following reference:
A.K. Datta, “Porous media approaches to studying simultaneous heat and mass transfer
in food processes. II: Property data and representative results, Journal of Food
Engineering, vol. 80, 2007
Best Regards,
Claire
Farjallah Alassaad
April 30, 2019Thank you for your reply and sorry again another question. yes i want to reduce the porosity but also let the relative humidity and the saturation the same as a 0.8 porosity of the example. just i don’t find the vapor pressure to change in the exercise, how can i change it and how much depending the porosity. sorry so much for disturbing.
Thank you
Francesco Borgognoni
July 2, 2019Hi Claire,
I am an MSc student and I am studying the process of drying of a bed of tea leaves, considering them as a porous media. I was wondering where I can find more information about the “evaporation flux” equation and what does the evaporation rate “K” represent.
Thank you,
Francesco.
bharathi raju
March 3, 2021Hi mam,
I need to analyze the change in Refractive Index of the hygroscopic material with the change in relative humidity. Please help me in this regards
Thanks in advance
R.Bharathi
Research Scholar
Iman
May 27, 2021Hi,
I would like to perform the 1000 hygrothermal calculations (heat and moisture transport calculations) for an external wall with COMSOL. I have 1000 data sets (The range of values for each parameter instead of one specific value) for the input parameters.
My question is:
Is it possible to input these 1000 data sets into COMSOL and perform these 1000 simulations automatically, OR am I need to input these inputs data one by one (manually) and perform 1000 simulations one by one?
Thanks a lot for your help and time.
Best regards,
Iman
MANIBHUSHAN KUMAR
June 6, 2023Please update me, if any event of workshop will be on Food processing.