Transdermal drug delivery (TDD) patches continuously deliver drugs into the body for a certain amount of time. However, the skin is designed to keep out foreign substances, like drugs. To create a TDD patch that successfully bypasses this barrier, simulation can be used to study drug release and absorption into the skin. To analyze this process, Veryst Engineering created a TDD patch model with the COMSOL Multiphysics® software and compared the results to experimental data.
Design Considerations for Transdermal Drug Delivery Patches
After a TDD patch is applied to the skin, it continuously delivers a low-level drug dose. This is beneficial when dealing with drugs with a rapid onset and short duration, like the pain medication fentanyl, because the patch releases the drug gradually over time. TDD patches are also more effective and convenient than traditional drug delivery methods.
Transdermal drug delivery patch. Image by RegBarc — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Designing TDD patches is a challenge for many reasons. One design challenge is that the skin is a little too good at protecting the body from foreign substances. To get drugs past the body’s natural defenses, the patch needs to contain a chemical permeation enhancer. The stronger the enhancer, the better it is at transporting the drug. But a stronger permeation enhancer is also more likely to irritate the skin. Therefore, when designing an optimal TDD patch, we must consider both its effectiveness and patient comfort.
To find a balance between these factors, we can analyze the drug diffusion process in a TDD patch with simulation. Alireza Kermani and Nagi Elabbasi from Veryst Engineering, a COMSOL Certified Consultant, demonstrated this by modeling a TDD patch in COMSOL Multiphysics and comparing the results to those from an experiment.
Modeling a TDD Patch in COMSOL Multiphysics®
To model the TDD patch, the researchers at Veryst Engineering first set up a 2D axisymmetric model. For their model, the skin and patch both have a thickness of 50.8 μm and the radius of the patch is 0.9 cm. The team also assumed that the drug and enhancer dissolve uniformly.

A cross section of Veryst Engineering’s TDD patch model, displaying the normalized initial drug concentration (not to scale). Image by A. Kermani and N. Elabbasi and taken with permission from their COMSOL Conference 2016 Boston paper.
The team then set up the appropriate physics and boundary conditions to accurately model the drug’s movement from the patch into the skin. They used a pointwise constraint in COMSOL Multiphysics to enforce the flux continuity and partitioning of the drug and enhancer at the interface. They also accounted for the nonlinear diffusion caused by the coupling of the drug and enhancer and specified the drug’s diffusion, which varies linearly with the enhancer’s concentration. Since drugs do not exit the top or sides of TDD patches, the team added boundary conditions to their model to stop the drug flux in those areas.
The lower boundary of the skin acts as a sink for both the drug and enhancer. Therefore, the concentration was set to zero at that boundary. This represents the drug and enhancer leaving the skin. Using a sink boundary condition means that the concentration is zero.
Next to the lower boundary of the skin is the dermis layer, which is not modeled in this research. However, the researchers still considered its effect. The dermis layer undergoes blood microcirculation, so when a drug reaches the lower boundary of the skin, it is removed via microcirculation and transferred to the rest of the body. The team assumed that the concentration of the drug or enhancer is zero at the skin’s lower boundary and added a sink boundary condition.
Analyzing the Drug Diffusion Process
The group at Veryst Engineering tested their model to see how it performed in three different cases:
- When there is no permeation enhancer in the patch
- When the permeation enhancer’s initial concentration is 0.08 g/cm3
- When the permeation enhancer’s initial concentration is 0.12 g/cm3
In all cases, the drug had an initial concentration of 0.06 g/cm3.
The drug diffusion process for the 2D model of the TDD patch. Animation courtesy of Veryst.
The simulation results show that the drug flux increases when there’s a permeation enhancer present, especially when it has a higher initial concentration. The plot below shows the normalized drug flux over time for the three enhancer concentrations.
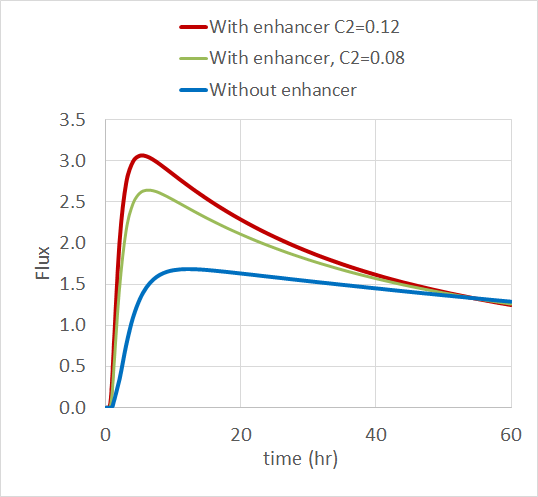
The normalized drug flux in the skin for the three levels of permeation enhancer concentration. Image courtesy of Veryst.
Comparing the Model to Experimental Results
The Veryst Engineering team validated their model by comparing the results to a previous experiment. The experiment used the drug fentanyl at a concentration of 0.06 g/cm3 and the permeation enhancer lauryl pyroglutamate at an initial concentration of 0.12 g/cm3.
Veryst’s model accounts for the maximum flux value in the TDD patch as well as how this value increases with a higher concentration of enhancer. However, the model doesn’t account for the flux’s broad peak and quick decay, which are investigated in the experiment. The simulation also does not predict the drug flux accurately over long periods of time.
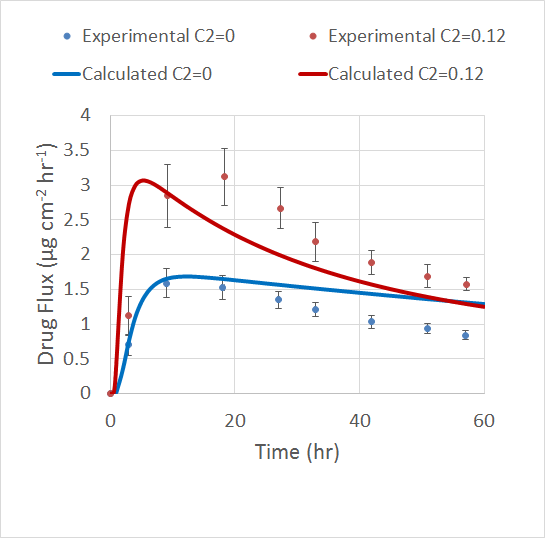
Comparison of the simulation results and experimental results for different permeation enhancer concentrations. Image courtesy of Veryst.
The engineers at Veryst suspect several factors may contribute to the difference in results. For instance, the Fickian diffusion model does not represent drug diffusion over a long period of time. Also, the assumption that drug diffusion increases linearly with a higher enhancer concentration is too simple to describe the drug diffusion process, which is time dependent. This means that the linear increase is not accurate for longer time periods.
Other components of the model, such as the boundary condition at the skin’s bottom layer, also need further investigation. A sink boundary condition for the enhancer may not be the right approach, since the solubility of the enhancer is not significant in the skin. On the other end of the spectrum, the team could have assumed that the enhancer has zero flux at the bottom boundary of the skin. The Zero Flux boundary condition increases the concentration of the enhancer in the skin, therefore increasing the drug flux. The true approach to describing this boundary is neither of these boundary conditions, but instead, something in between.
Another aspect to consider moving forward is the hydration in the skin and patch. The skin sample in the experiment is fully hydrated and when the patch is applied, the patch hydration level increases. The patch begins to swell, changing the concentrations of the drug and enhancer. This effect is not accounted for in the model.
Next Steps for Modeling a TDD Patch
The model designed by the team at Veryst Engineering demonstrates that, with additional information, it’s possible to simulate TDD patches in COMSOL Multiphysics. According to the team, the COMSOL software made it easy to include the continuity of flux, partitioning of the drug and enhancer, and the effect of coupling the drug’s diffusion coefficient with the concentration of the enhancer.
To get an accurate representation of the diffusion process, more research needs to be done on selecting the appropriate boundary conditions as well as choosing the correct factors to investigate, including hydration.
After building an optimized TDD patch model for future research, it is possible to couple it with other types of physics. For example, we can account for heat transfer in the patch model to determine how heat affects the drug diffusion process.
Additional Resources
- Learn more about Veryst Engineering
- Read the full paper from the COMSOL Conference 2016 Boston: Transdermal Drug Delivery with Permeation Enhancer
- Browse the COMSOL Blog to see more about how Veryst uses simulation:





Comments (1)
Marcela Mercado Montoya
July 23, 2021Dear Bridget,
Thank you for this blog. Did you consider the molecular weight of Drug and Enhancer to use the Transport of Diluted Species interface from Comsol?
Best regards