
Previous work on cloaking for flexural waves in elastic plates presented limitations and near invisibility. Now, a research group in Europe has figured out a new theoretical framework to both overcome the limitations and achieve exact cloaking for flexural waves in Kirchhoff-Love plates. To visualize and test the quality of the cloak, they ran COMSOL Multiphysics simulations.
A Brief Explanation of Cloaking Transformations
Picture this: There are flexural waves emanating from a source in a thin elastic plate. If you place an object in the plate, it will disturb the waves and you will be able to see it. If a cloak is instead placed around the object, the waves will not be disturbed, thus rendering the object invisible.
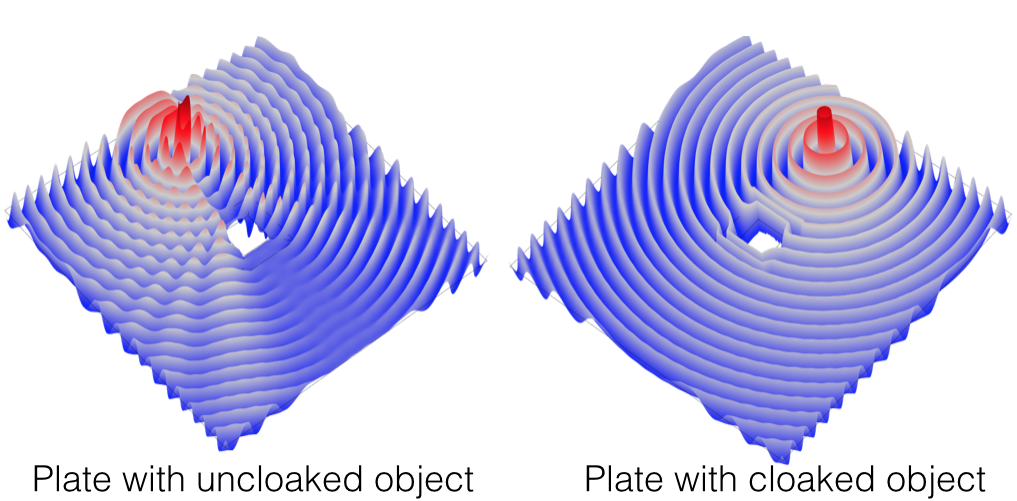
Models illustrating an object without and with cloaking. Provided by Daniel J. Colquitt.
While that’s an easy enough concept to grasp, it is not so easy to realize. In order to cloak an object, you need to construct the right metamaterial (metamaterials do not exist in nature; they are artificial materials, engineered to have specific properties).
Metamaterials can be designed such that their material properties mimic the spatial variations created by coordinate transformations, thereby directing light, sound, or other waves in a specific manner. The initial configuration of the electromagnetic or acoustic fields is mapped on a Cartesian mesh, which is then twisted to transform the coordinates.

Illustration of an untwisted Cartesian mesh.
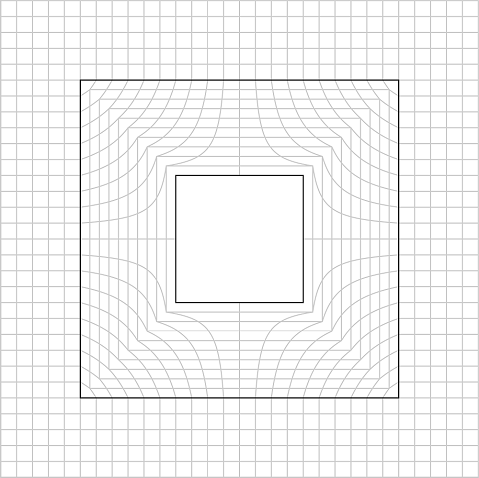
Twisted mesh. Provided by Daniel J. Colquitt.
Cloaking Light and Sound
When it comes to electromagnetic and acoustic cloaking, you would use Maxwell’s equations and the Helmholtz equation, respectively. Both of these equations are invariant when coordinates transform, meaning they are not altered in the process.
Cloaking Mechanical Waves
However, if you want to mathematically model cloaking for mechanical waves, such as flexural waves in elastic plates, you need a fourth-order partial differential equation (PDE). The general form of the PDE is not invariant; it changes during the coordinate transformation.
Earlier work with applying transformation elastodynamics to achieve cloaking came with strings attached. Following some previous frameworks, calculations yielded tensorial densities and nonsymmetric stresses. Other research produced a framework where the PDE could be applied to thin plates, but only for nonlinear theories.
COMSOL Multiphysics user Daniel J. Colquitt and his colleagues are finally breaking through the limitations of this type of cloaking design.
Overcoming the Limitations: Cloaking for Flexural Waves in Elastic Plates
In the paper “Transformation elastodynamics and cloaking for flexural waves”, D.J. Colquitt, M. Brun, M. Gei, A.B. Movchan, N.V. Movchan, and I.S. Jones present a new framework for transformation elastodynamics for thin plates and an algorithm for broadband cloak design. The thin elastic plates are represented by Kirchhoff-Love plates — a 2D mathematical model that is commonly used to characterize thin plates.
“The equations which govern the flexural displacement of thin elastic plates are very different to those for light and acoustics (e.g., Helmholtz equation),” Colquitt explained to me in an email conversation. He added, “Indeed, the equation of motion for flexural waves involves the biharmonic operator, which is a fourth-order partial differential operator; this is fairly unusual for physical systems where the equations of motion are usually first- or second-order in space (e.g. Electromagnetism, Acoustics, Elasticity).”
So how did the researchers overcome the issue of equation variance during the coordinate transformation? They gave the transformed equation a physical interpretation by introducing a generalized plate model. In this new framework, the invisibility cloak is created by applying a specific combination of pre-stress and body forces to a metamaterial plate. Unlike other frameworks, the new one is completely linear. They also show that their new algorithm successfully ensures symmetric stresses and scalar densities.
The Power of Entering Your Own Equations
To visualize the cloaking results and test the quality of the cloak, Colquitt et al. created simulations using COMSOL Multiphysics software. Apparently, when deciding which software to use for testing out their cloak, flexibility was a key factor.
“The invisibility cloak requires the implementation of an inhomogeneous, anisotropic plate subjected to inhomogeneous and anisotropic pre-stress and body forces. As one can imagine, the governing equations for this system are nonstandard,” Colquitt said. “COMSOL allowed us to directly implement the precise form of the transformed governing equations. This is very attractive for a mathematician — the ability to directly control the system of equations being solved.”
Below are some images and an animation illustrating their results.
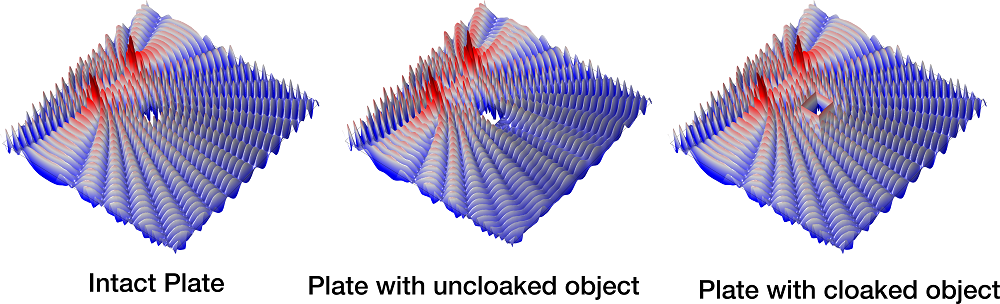
Cloaking results. Provided by Daniel J. Colquitt.
Animation of the square cloaked object moving in the flexural waves in the thin plate. Courtesy of Daniel J. Colquitt.
Research Applications
So, the researchers have successfully developed a new theoretical framework that will allow experimentalists to design and build mechanical invisibility cloaks that can hide or protect objects from mechanical vibrations.
As far as putting the framework to use, Colquitt said: “There are many potential applications, such as cloaking, or the isolation of sensitive pieces of equipment from mechanical vibrations by routing the flexural waves around the equipment.”
In short, this is very fascinating research and I highly recommend reading the paper (link below) to get the full scope of their work.
Further Reading
- Read the paper “Transformation elastodynamics and cloaking for flexural waves” at ScienceDirect
- More research by D.J. Colquitt et al.: “Making waves round a structured cloak: lattices, negative refraction and fringes” from The Royal Society of London





Comments (3)
Michele Brun
May 5, 2016I also suggest the reading of the paper:
Brun, M., Colquitt, D., Jones, I.S., Movchan, A.B., Movchan, N.V. 2014 “Transformation cloaking and radial approximations for flexural waves in elastic plates” New J. Phys., 16, 093020.
doi: 10.1088/1367-2630/16/9/093020
Michele Brun
May 5, 2016I also suggest the reading of the open source paper.
Brun, M., Colquitt, D., Jones, I.S., Movchan, A.B., Movchan, N.V. 2014 “Transformation cloaking and radial approximations for flexural waves in elastic plates” New J. Phys., 16, 093020.
doi: 10.1088/1367-2630/16/9/093020
芝祺 刘
April 6, 2020您好,我在进行二维声子晶体板波能带结构的仿真过程中遇到一些问题,想要请教您。
在仿真过程中我想要去掉其中的反对称型兰姆波的模态,唯一对对称型兰姆波的能带结构进行分析,我该如何在comsol中设置来实现这一目的。
谢谢。