
When designing multibody systems, interconnected flexible and rigid bodies must be analyzed to see how they are affected by large rotational and translational displacements. While we can achieve this with the Multibody Dynamics Module in the COMSOL Multiphysics® software, we first want to confirm the reliability of the simulation results. Here, we discuss a benchmark model of a four-bar mechanism that helps prove the validity of these multibody dynamics simulations.
Analyzing Defects in Multibody Systems
Multibody systems involve multiple rigid or flexible bodies that are connected to each other and may be subjected to large displacements. Such systems have applications in the aerospace industry and robotics and are used to create machines such as helicopter swashplate mechanisms and reciprocating engines.

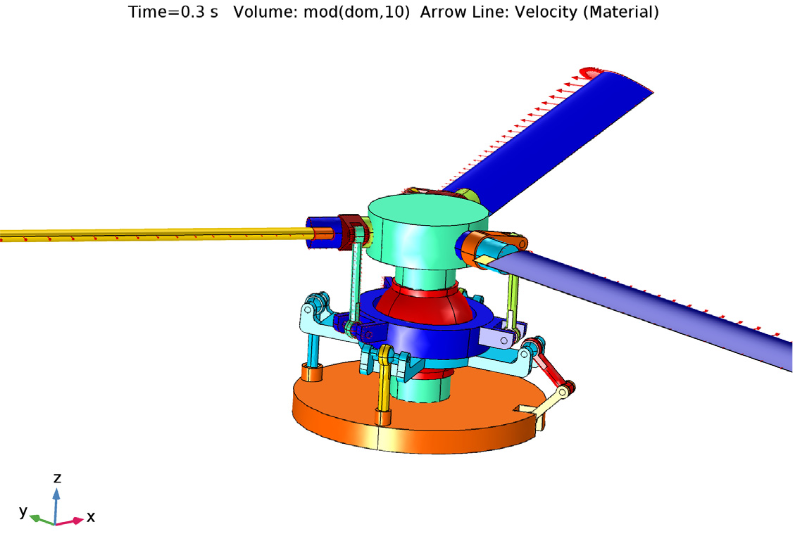
A helicopter and helicopter swashplate, an example of a multibody system. Left image by Riley Kaminer — Own work. Licensed under CC BY 2.0, via Flickr Creative Commons.
When designing multibody systems, engineers need to detect and avoid defects, thereby preventing future issues and optimizing their designs. They can achieve this by performing simulation analyses with the Multibody Dynamics Module, an add-on product to COMSOL Multiphysics and the Structural Mechanics Module. To confirm the reliability of these simulations, engineers can benchmark their results against existing data.
Here, we’ll show you a benchmark example of a four-bar mechanism, which is used in bicycles, for example. We analyze the mechanism’s dynamic behavior with the Multibody Dynamics Module and check how well the results compare to existing research. With this benchmark model, we hope to show that the results generated by the Multibody Dynamics Module can be relied on for these types of analyses.
Modeling a Four-Bar Mechanism with COMSOL Multiphysics®
Looking at the geometry of the planar four-bar mechanism example, we see that it consists of three links (labeled Link 1–3). The mechanism has a defect so modeling these links as rigid causes the mechanism to lock. Instead, we model them as flexible parts via the Linear Elastic Material node where Link 1, the mechanism’s left crank, has an angular velocity of 1 rad/s.
Connecting these links are four hinge joints (labeled Hinge joint 1–4), which are located at points A–D in the image below. Hinge joints 2 and 3 (located at points B and C, respectively) connect Links 1 and 3 to Link 2. Meanwhile, Hinge joints 1 and 4 (located at points A and D, respectively) connect Links 1 and 3 to a fixed constraint.
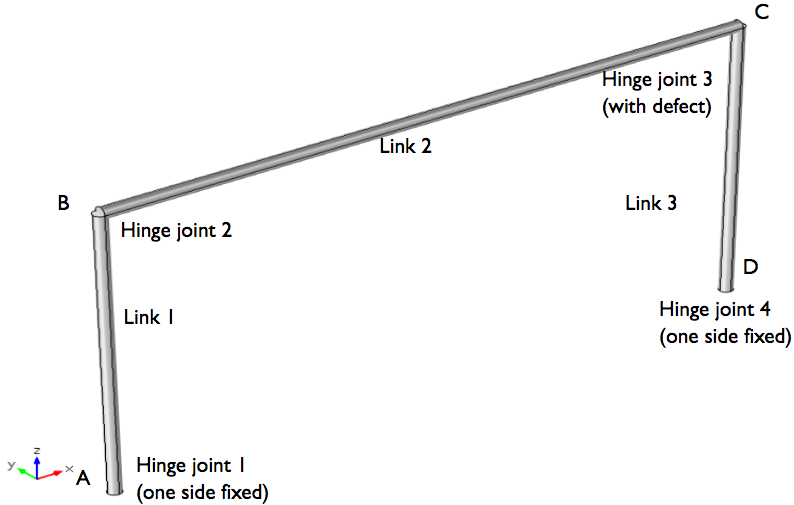
The geometry of the four-bar mechanism model. Here, Links 1 and 3 are 0.12 meters long, while Link 2 is 0.24 meters long. All of the links have a circular cross section with a diameter of 5 millimeters.
Without a defect, the mechanism model would only move within the plane, as the four hinge joints would have an axis of rotation that is perpendicular to the mechanism’s plane. However, in this model there is an assembly defect in Hinge joint 3 (point C). This alters the joint’s angle of rotation, skewing it 5° from the normal to the plane. As a result, the mechanism experiences out-of-plane motion.
Validating the Multibody Dynamics Benchmark Model with an Existing Study
Using this model, we can study the displacement caused by the four-bar mechanism’s defect and validate our results against an existing study. First, we plot the mechanism’s displacement and trajectories for Points B (a hinge joint without a defect) and C (the hinge joint with a defect) after 10 seconds. By doing so, we see how the assembly’s defect affects the trajectories in a four-bar mechanism.
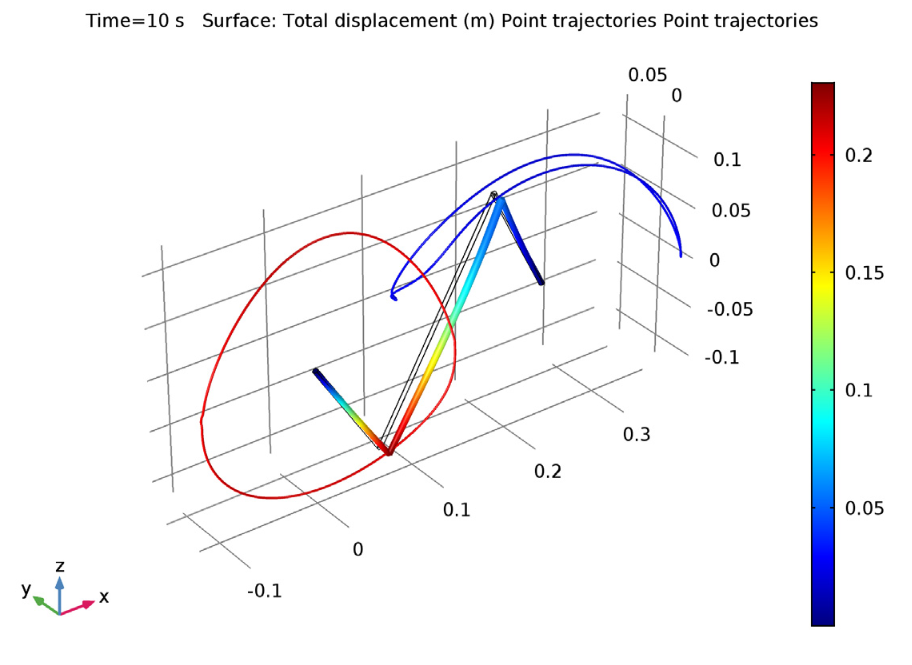
The four-bar mechanism model after 10 seconds, showing the trajectories of points B and C during those 10 seconds. The visualization is enhanced by scaling the out-of-plane displacement by a factor of 20.
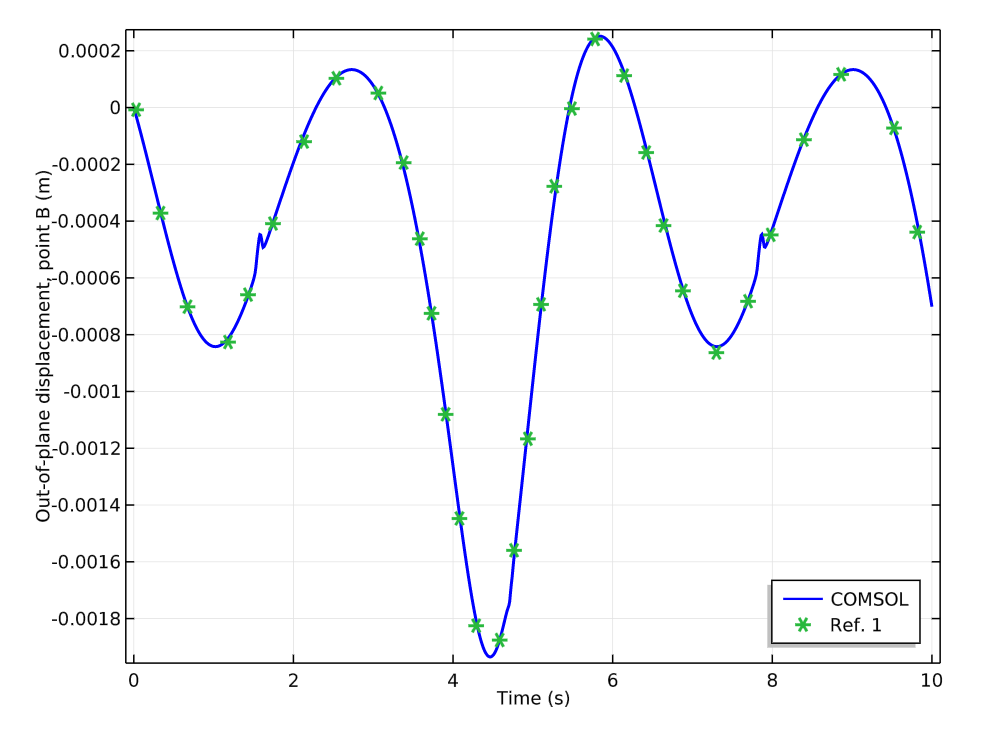
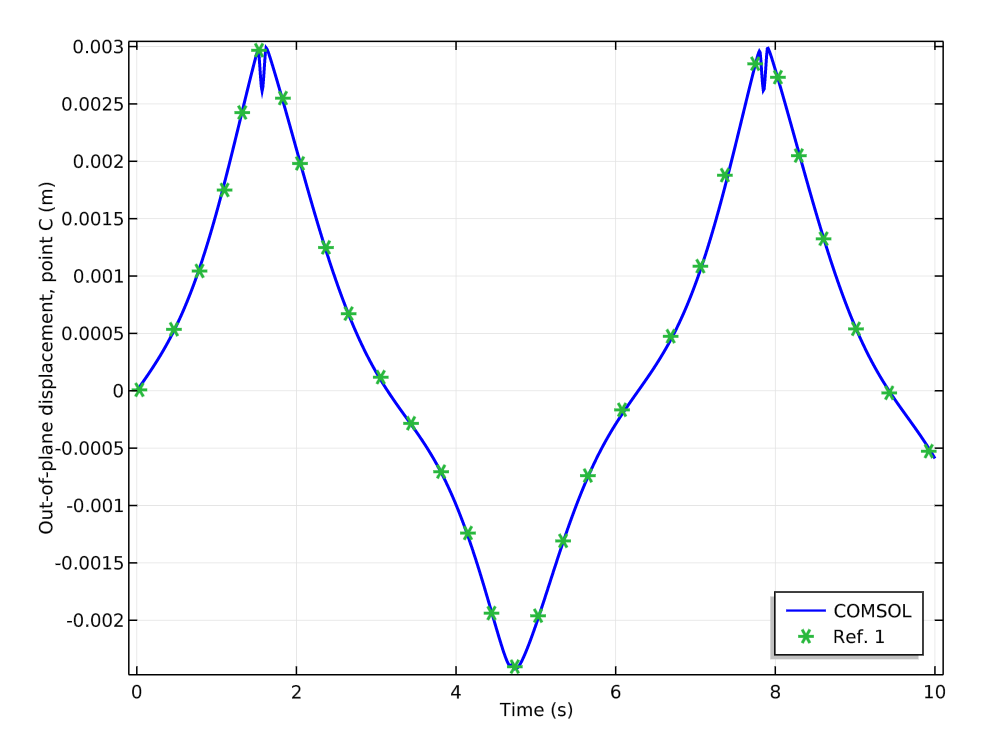
Next, we compare the simulation results for out-of-plane displacement to an existing study (Ref. 1 in the model documentation). In our comparison, we study the displacement’s y-component at points B and C.
The comparison shows that the computed results are in very good agreement with the results from the reference. Further, both the computed and existing results confirm that the out-of-plane displacement vanishes when there is no defect in the joint.
Comparison of the out-of-plane displacements for points B (left) and C (right) between the COMSOL Multiphysics model and reference.
With this benchmark model, we demonstrate that we can confidently use the Multibody Dynamics Module to generate verifiable results.
Learn More About Analyzing Multibody Dynamics Applications
- Browse other blog posts related to modeling multibody dynamics:




Comments (0)